石子合并模拟
主题
本作品通过可视化的方式模拟石子合并问题，展示不同算法（正解for循环的dp，记忆化搜索以及非记忆化搜索的解法及其复杂度对比、非正解的类哈夫曼编码的贪心做法的局限性），帮助用户深入理解算法思想。
在线预览
作品特色/难点/创新点
- 自定定义的 石子合并模拟
- 回溯 最优解的 合并过程
- 记忆化搜索 和 非记忆化搜索 的复杂度可视化对比
- 可视化 类哈夫曼编码的贪心解法，初学时的错误解法
作品内容详细描述
本作品主要包含以下内容：
1. 回溯最优解的合并过程
通过动画展示最优解的合并路径，帮助用户直观理解算法的执行过程。 实现：
在dp方程转移时保存最优解即可
ai想的更聪明一些，只用 split[i][j] 来记录 合并 [i,j]最优解的分割点 k，而本人最初的想法比较笨，用 split[i][j] 来记录 合并 [i,j]最优解的 两个合并区间 [[i,k],[k+1,j]]
通过回溯函数 generateSteps，根据 steps 数组重建最优合并路径
[
{
"left": 0,
"right": 1,
"cost": 4,
"description": "合并区间 [0, 0] 和 [1, 1]，代价: 4",
"mergedStones": [
1,
3,
3,
2,
4
],
"mergeLeft": 0,
"mergeRight": 1,
"splitPoint": 0,
"intervals": [
{
"start": 0,
"end": 0
},
{
"start": 1,
"end": 1
},
{
"start": 2,
"end": 2
},
{
"start": 3,
"end": 3
},
{
"start": 4,
"end": 4
}
],
"highlightIndices": [
0,
1
]
},
{
"left": 0,
"right": 2,
"cost": 7,
"description": "合并区间 [0, 1] 和 [2, 2]，代价: 7",
"mergedStones": [
4,
3,
2,
4
],
"mergeLeft": 0,
"mergeRight": 2,
"splitPoint": 1,
"intervals": [
{
"start": 0,
"end": 1
},
{
"start": 2,
"end": 2
},
{
"start": 3,
"end": 3
},
{
"start": 4,
"end": 4
}
],
"highlightIndices": [
0,
1
]
},
{
"left": 3,
"right": 4,
"cost": 6,
"description": "合并区间 [3, 3] 和 [4, 4]，代价: 6",
"mergedStones": [
7,
2,
4
],
"mergeLeft": 3,
"mergeRight": 4,
"splitPoint": 3,
"intervals": [
{
"start": 0,
"end": 2
},
{
"start": 3,
"end": 3
},
{
"start": 4,
"end": 4
}
],
"highlightIndices": [
1,
2
]
},
{
"left": 0,
"right": 4,
"cost": 13,
"description": "合并区间 [0, 2] 和 [3, 4]，代价: 13",
"mergedStones": [
7,
6
],
"mergeLeft": 0,
"mergeRight": 4,
"splitPoint": 2,
"intervals": [
{
"start": 0,
"end": 2
},
{
"start": 3,
"end": 4
}
],
"highlightIndices": [
0,
1
]
}
]- 根据 steps 可视化过程即可,但是ai在这一步却始终不能只靠自己来修复bug，由于石子的位置在合并过程中会发生变化，所以需要在每次合并后更新石子的位置，确保可视化的正确性。
具体做法
做法1.
在每次模拟的时候，用 结构体{st,ed} 来存储 石子的区间信息，在每次合并时候，这个数组也跟着模拟，并且，可以通过 每次模拟时候扫一遍数组，就可以知道 这个 两个合并的区间具体在这次模拟中处于石头的什么位置 初始情况 ，假设有3堆石头 [1, 2, 3]，那么初始的区间数组为：
[
{ start: 0, end: 0 }, // 石子1
{ start: 1, end: 1 }, // 石子2
{ start: 2, end: 2 } // 石子3
]最优解的合并 为 [0,0] & [1,1]
[
{ start: 0, end: 1 }, // 合并后的石子1和石子2
{ start: 2, end: 2 } // 石子3
]最优解的合并情况为 [0,1]&[2,2]我们只需要扫一遍数组，就可以知道 [0,1]和[2,2] 在这次模拟中处于石头的什么位置。更具体一点，我们只需要找到 [0,1]的位置即可
做法2
我们将合并过程看出一颗树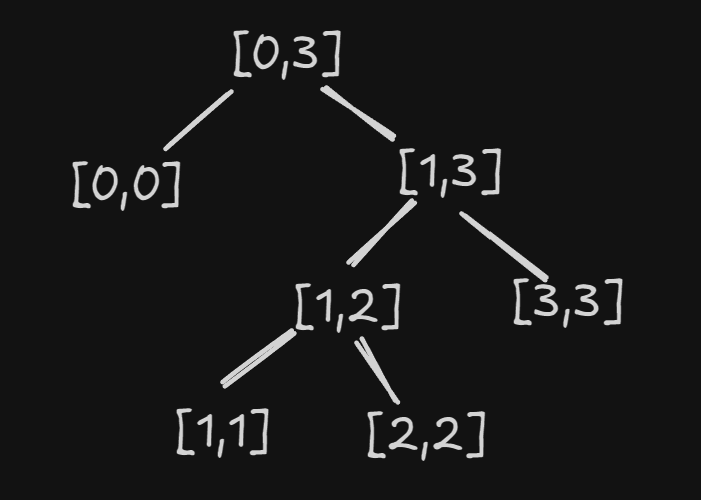 
当最优解中某一步 为 [l1,r1] [l2,r2] 时，我们想要知道 [l1,r1] [l2,r2] 在什么位置，由于这两区间相邻，我们只要关注[0,l1-1] 区间内有多少石头即可,又因为每次合并[l1,r1] [l2,r2] 会让[l1,r2] 的石头数-1,更进一步，因为 合并[l1,r1] [l2,r2]后，不可能有后续的合并操作发生在[l1,r2]中，所以我们看作 只对 l1这个位置的石子数-1,之后我们就可以用 树状数组等数据结构来维护[0,l1]区间内的石子数了。 这样的做法复杂度更低
但是 在石头上标注区间的会使得可视化更加清晰，最终还是选择做法1
2. 记忆化搜索与非记忆化搜索的对比
通过可视化对比两种方法的效率差异，帮助用户理解记忆化搜索的优势。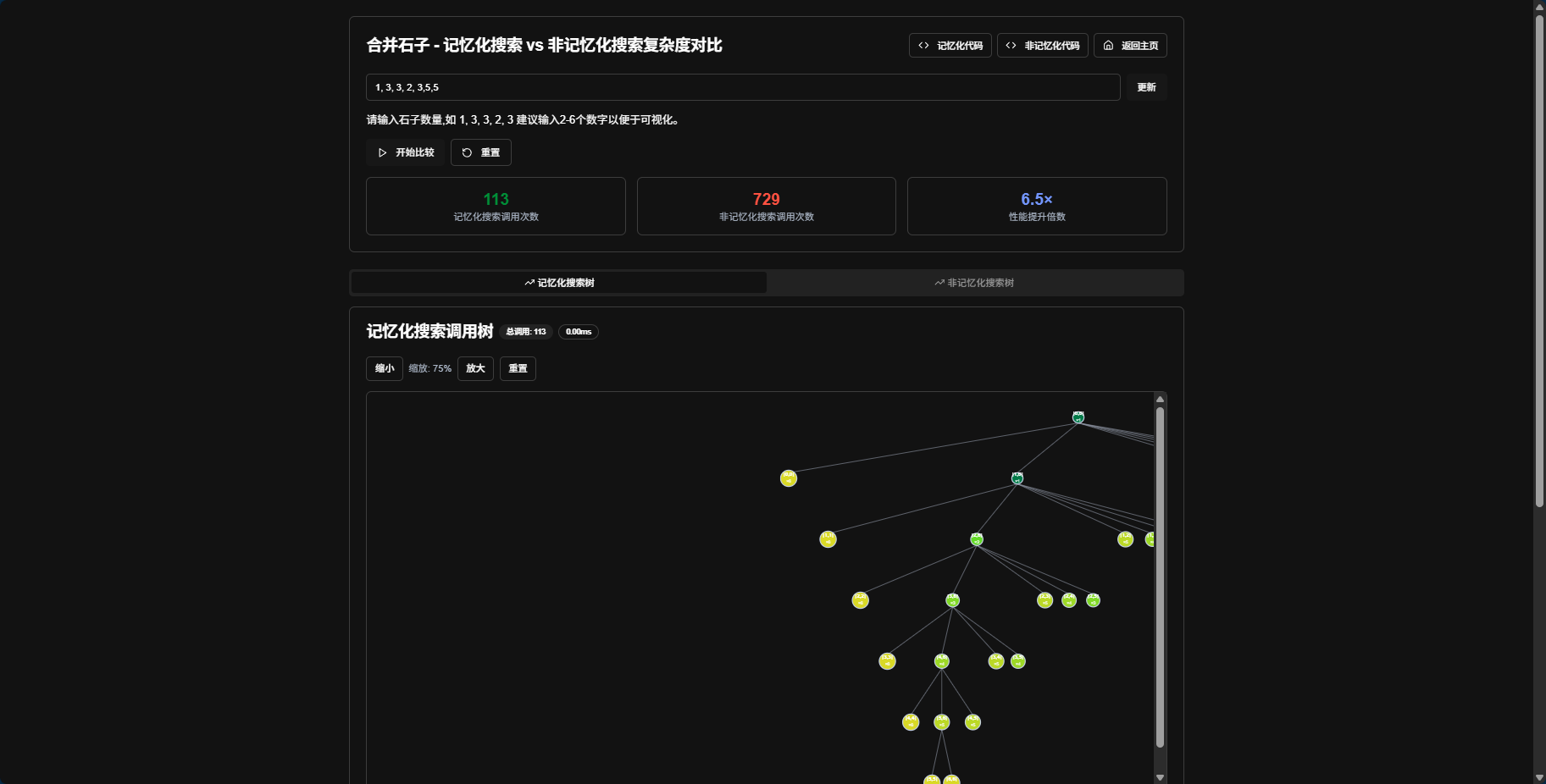 
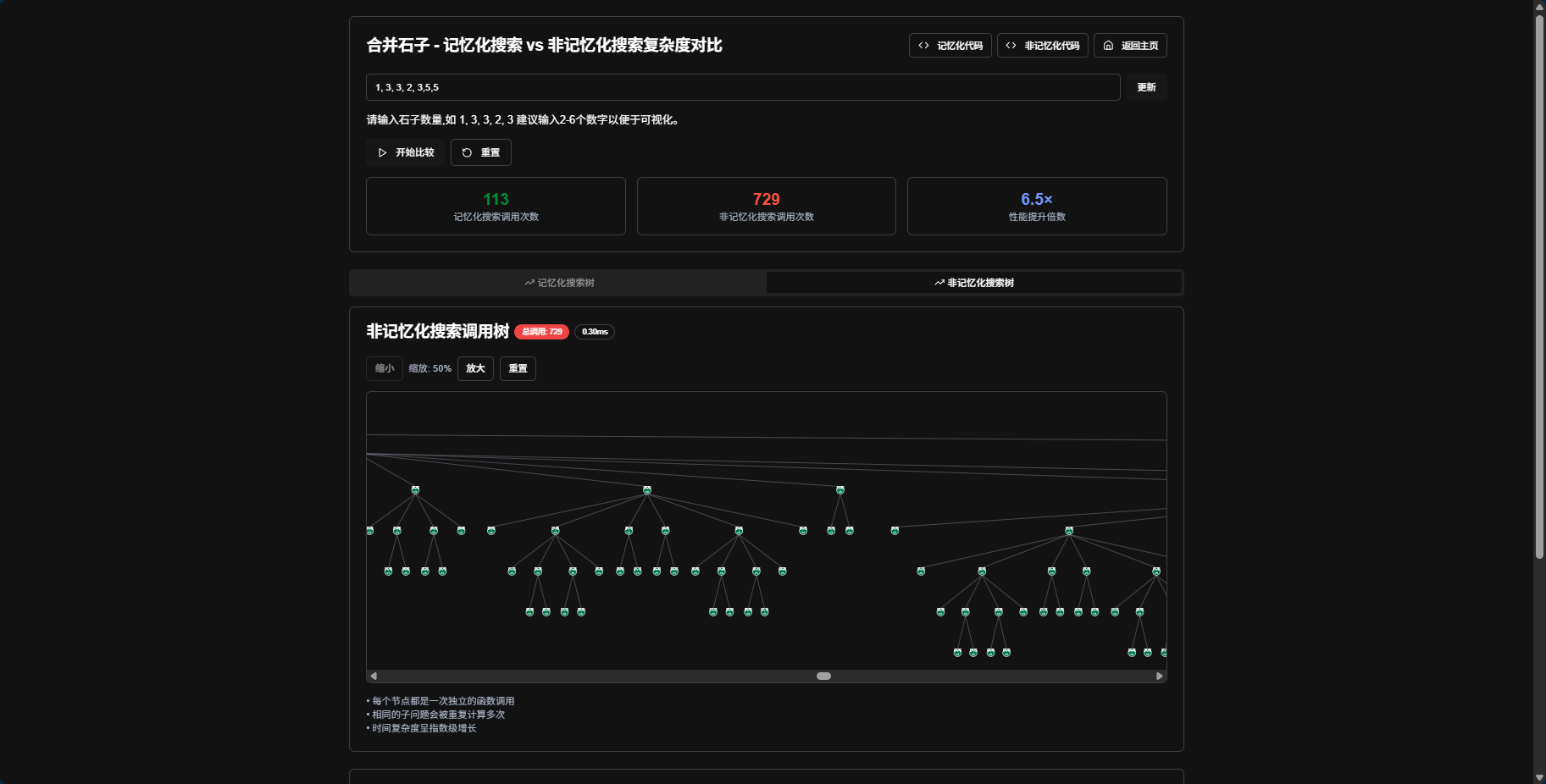ps: 聪明的ai没想到在样式上始终不能只靠自己来修复bug， 可能是我说的的不够准确，svg的图可能会过大，导致树无法完成显示，提供具体解决方案( dfs时候计算深度常量 和 第一层的宽度 作为svg的宽度 和 深度常量作为svg的高度 最后在svg的 container设置 overflow: auto;属性 )后，ai便轻松解决
3. 错误解法的演示
展示类哈夫曼编码的贪心解法，分析其局限性和错误之处。
运行
- 安装依赖
npm install pnpm -gpnpm instal- 启动项目
pnpm run dev